Rory Smith, ThyssenKrupp Elevator Inc., USA
Richard Peters, Peters Research Ltd., UK
Key Words: Simulation, dispatching, destination dispatch, boosters, energy, TWIN, Vmax
This paper was presented at ELEVCON ISTANBUL 2004, The International Congress on Vertical Transportation Technologies and first published in the IAEE book “Elevator Technology 14”, edited by A. Lustig. It is reproduced with permission from The International Assocication of Elevator Engineers. This web version © Peters Research Ltd 2009.
Abstract
ETD, Estimated Time to Destination, is a patented ThyssenKrupp Elevator algorithm which can be used in three modes: (i) destination dispatch, (ii) conventional dispatching with up/down hall call buttons, (iii) a combination of destination input on busy floors, with conventional hall call buttons on other floors. Improvements have been made to the ETD optimization function so that it can adjust the relative importance of waiting and transit times. Other optimization parameters can be introduced, such as a function to minimize the energy consumption arising from alternative dispatching decisions. ETD is also being adapted to the Vmax controlled over-speed technology, and to TWIN, which utilizes two cars in one shaft.Current methods for calculating lift energy consumption rely on rules of thumb and generalisation. The accuracy of these models is very limited. In this paper a new general energy modeling approach is proposed. This approach has been applied to design a new lift energy model, which can be used to calculate the energy consumption of any individual lift trip. The energy model is linked to a lift traffic simulation program, which enables the energy consumption of a lift installation to be calculated in any building, and for any passenger traffic scenario.
1. Introduction
The patented ThyssenKrupp ETD (Estimated Time to Destination) dispatching concept was presented at Elevcon 2002 [1], together with simulation demonstrations using the non-proprietary elevator simulation software, Elevate[TM]. ETD as described at Elevcon 2002 is currently available with the ThyssenKrupp TAC50 control system. This paper describes some additional enhancements to ETD, again supported by Elevate simulation results.
ETD can operate as a full destination control system, where passengers register their destination floors at landings. ETD can also operate with conventional up/down hall call buttons, or with a combination of up/down hall call buttons and “booster” destination call stations on peak floors. For systems without destination input, ETD infers the number of people behind each hall call, and probable future car calls based on traffic learning algorithms.
ETD aims to minimize total passenger time to destination, which is the time passengers are waiting for and traveling in the elevators. It takes account of the time it will take for each elevator to serve the new call. It also takes full account of the impact of the new allocation on all other passengers in the system.
To understand how the ETD algorithm differs from other algorithms, consider the following scenario: there are three elevators, and a number of calls on the system. A new down hall call is registered at level 7. Which elevator should serve the call?
A conventional ETA (Estimated Time of Arrival) dispatching decision is presented in Figure 1.
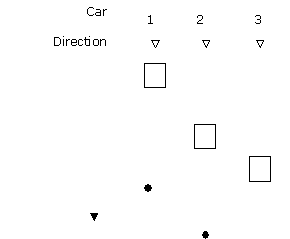
Car 1 is 15 s from the call. It has to stop at level 8, which will delay it 10 s on its journey to level 7. So the ETA of Car 1 is 15 s plus 10 s, which is 25 s.
Car 2 is 10 s from the call.
Car 3 is 5 s from the call.
Based on the above analysis, the ETA algorithm allocates Car 3.
Figure 1 Example allocation using an ETA dispatcher
A Fuzzy Logic or other intelligent controller may make a more sophisticated analysis, as suggested in Figure 2.
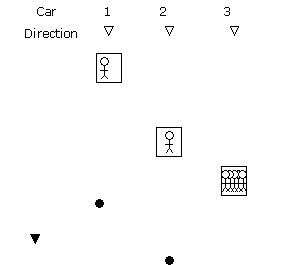
There are many variations in implementation, but the deciding logic may be as follows:
Car 1 is far and almost empty
Car 2 is close and almost empty
Car 3 is very close and almost full.
Car 2 is allocated in preference to Car 3 as the more intelligent controller realizes that minimizing ETA is not always the best strategy. It is worse to delay the almost full car to pick up the new passenger, even though it is the closest.
Figure 2 Example allocation using a Fuzzy Logic or other intelligent dispatcher
Using ThyssenKrupp ETD the analysis is as follows in Figure 3.
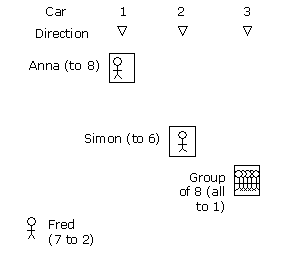
If Fred is allocated to Car 1, then
- The delay to Anna is 0 s.
- Fred waits 15 s for the elevator to travel to him, plus 10 s to drop off Anna.
- Once picked up, Fred then has to complete his journey, which will take 25 s.
- The Total Cost is 50 s.
If Fred is allocated to Car 2, then
- Simon’s trip is delayed by 10 s while Fred is picked up.
- Fred has to wait 10 s to be picked up.
- Fred then takes 25 s to complete his journey, plus 10 s to drop off Simon.
- The Total Cost is 55 s.
If Fred is allocated to Car 3, then
- A group of 8 people are each delayed 10 s to pick up Fred and 10 s to drop off Fred.
- Fred has to wait 5 s to be picked up.
- Fred takes 25 s to reach his destination once he has been picked up.
- The Total Cost is 190 s.
Fred is allocated to Car 1, as this allocation is the best overall solution.
Figure 3 Example allocation using an ETD dispatcher
Figures 1 to 3 are only indicative of how the different systems may evaluate the same scenario and make a different decision. For other scenarios, the different systems may or may not make the same allocation.
2. ETD optimization function
The goal of the ETD optimization algorithm is to minimize the total time to destination. Consider the scenario where the dispatcher is choosing between the allocation options which will give rise to the waiting and transit times given in Table 1 and Table 2.

Table 1 Predicted waiting, transit and time to Destination for allocation option A
Table 2 Predicted waiting, transit and time to destination for allocation option B
Note that allocation option A gives a total time to destination less than allocation option B. Thus option A would be selected by standard ETD. However, Anna is being penalized by giving Fred excellent service. The overall perceived level of service may be better if we selected allocation option B. This raises a number of questions: (i) What is more “painful” for passengers, waiting time or transit time. (ii) Is the 1st second of waiting time less painful than the 15th or the 155th second?
To optimize the perceived level of service, we need a way of defining how undesirable each additional second of waiting or transit time is. One way to achieve this is to use a “pain index” to define the relative importance of waiting and transit times. And then select allocations to minimize the “pain”. The technique, which is akin to Fuzzy Logic, is very flexible. For example, conventional ETD, minimizing strictly on “time to destination” could be represented by the graphs in Figure 4. Applying these graphs, a passenger waiting 10 seconds and traveling for 50 seconds experiences 60 units of pain.
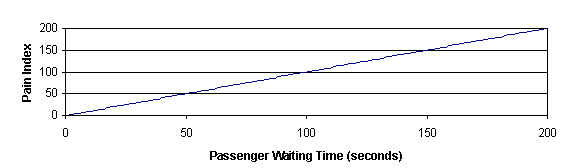
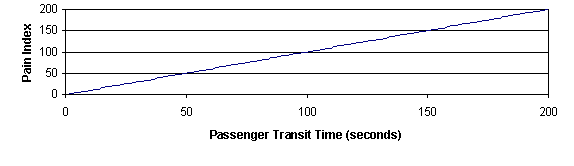
Figure 4 Optimization functions based on original ETD
If we considered waiting time to be three times as painful as transit time, then the optimization functions could be represented as shown in Figure 5. In this instance a passenger waiting 10 seconds and traveling for 90 seconds would experience 40 units of pain.
Figure 6 shows an optimization function taking into account the hypothesis that the initial 10 seconds of waiting and 30 seconds of transit time are of minimal concern. After this, each additional second of waiting is more painful than the last. The curve is not exponential. This avoids an overloaded system degrading to the point where it is always chasing the oldest call; which then creates even more old calls.
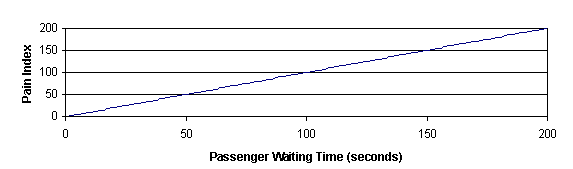
Figure 5 Optimization functions where waiting time is three times as painful as transit time
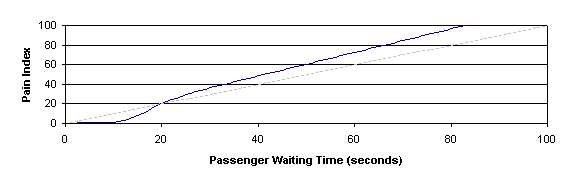
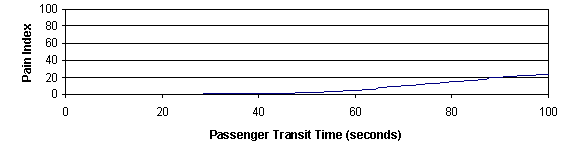
Figure 6 Optimization functions based on subjective opinions about the importance of waiting and transit times
The choice of optimization function is a subjective decision. The selection may be different according to building type and culture. To allow for this, the commercially available ETD algorithm will allow the customer to choose either a preset optimization function, or to define the function precisely.
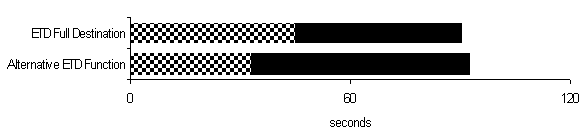
Figure 7 shows average waiting and transit time results for a benchmark lunchtime simulation [1] where a heavy 15% of the traffic is being transported per 5 minutes. The original ETD Full Destination is optimizing on time to destination, and achieves this goal. The Alternative ETD Function is based on ETD Full Destination, but using the optimization function described in Figure 5, where waiting time is more important than transit time. As a result we are achieving significantly better waiting times. However, the price is a slightly longer total time to destination.
 Average Waiting Time (s)
Average Waiting Time (s) Average Transit Time (s)
Average Transit Time (s)
Figure 7 Simulation results for benchmark lunchtime simulation
3. Energy optimization
The ThyssenKrupp energy model developed by Al Sharif et al [2] has been integrated into the ETD dispatcher. Applying the energy model we can predict, in advance of making the allocation of a call to an elevator, the energy consumption arising from each alternative dispatching option.
Using the new optimization strategy available for ETD, we can control how important energy consumption is relative to the waiting and transit times of passengers. The pain function will always be a straight line as each additional joule of energy costs the same; there is not an issue with perception as there is with waiting and transit times. The optimization function is then represented by three graphs. The first two may be as given in Figures 4 to 6. The third introduces the energy cost, as per the example in Figure 8.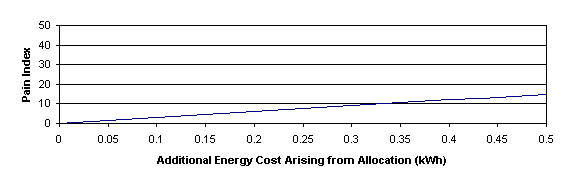
Figure 8 Example optimization function for energy cost
The energy pain function could be varied dynamically during the day to raise performance in peak times, and focus more on reducing energy consumption at other times of the day. Figure 9 shows average waiting and transit time results for a benchmark lunchtime simulation [1]. The simulations have been repeated with the energy pain function set at different gradients. As would be expected, there is a tradeoff between energy savings and performance.
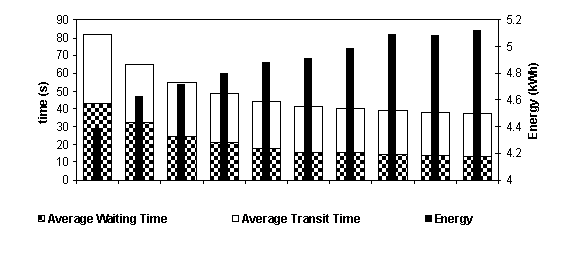
Figure 9 Graph to demonstrate trade off between energy saving and traffic performance
4. VMAX
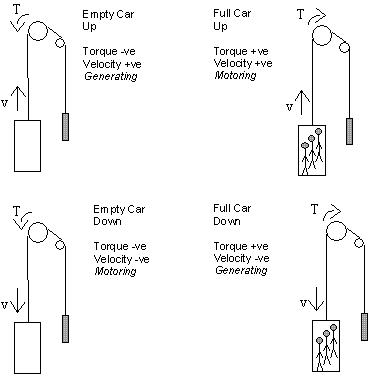
Figure 10 Elevator drives operating in 4 quadrants
When an elevator leaves the ground floor full of passengers, it is motoring, requiring predominantly positive torque in a positive direction. As passengers are dropped off up the building, the counterweight becomes heavier than the elevator, so the motor is providing predominantly negative torque in a positive direction. Similarly for a journey down the building, a negative direction, the motor can be required to deliver both positive and negative torque.
Thus the elevator is said to operate in “four quadrants”, as represented graphically in Figure 10.
Assuming a conventional counterbalancing ratio is less than 50%, an elevator works hardest when it is travelling up and is fully loaded. At other times, the system is required to motor or to generate with less torque. It should be noted that an elevator lift car fully loaded with passengers is only carrying about 65% of its rated capacity. Vmax is the name given to the concept of over-speeding the car when we have “spare” torque available.
Equation 1 is conventionally applied to calculate the design power of a drive motor in an elevator.
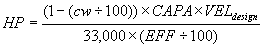 (1)
(1)
where
- HP Power (in horsepower)
- cw Counterweight (as a % of the maximum car capacity
- CAPA Maximum car capacity (lbs.)
- VELdesign Pre-set design velocity of the elevator (fpm)
- EFF Efficiency of the elevator (%)
The maximum theoretical velocity for an individual is determined by applying Equation 1 in reverse. Before the trip commences, the actual passenger load in the car Lactual is measured. Velopt, the optimized velocity is then determined using equation 2.
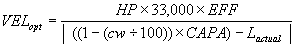 (2)
(2)
The maximum velocity for any journey between any two predefined floors is then selected from the lowest of three velocities as follows:
- The maximum velocity attainable according to Equation No. 2
- The maximum velocity attainable for the distance between the two floors. This distance is defined by the acceleration rate and jerk rates, motor and drive capabilities, and by human comfort factors
- The maximum velocity attainable with the mechanical equipment selected for the elevator.
Figure 11 shows the down peak performance for a benchmark building [1] with and without Vmax. A counterweight ratio of 50% and a maximum over speed of 30% has been assumed.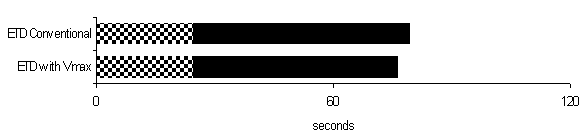
 Average Waiting Time (s)
Average Waiting Time (s) Average Transit Time (s)
Average Transit Time (s)
Figure 11 Example down peak performance with and without Vmax
5. ETD Applied to twin
The ThyssenKrupp TWIN system presented by Thumm [3] allows two independent elevators to run in a single shaft. In appropriate applications, this has the potential for dramatic savings in core space. The ETD algorithm has been extended to control these cars efficiently. TWIN ETD currently assumes destination input on every floor.
Running two cars in a single shaft presents some unique challenges in dispatching technology. The ETD strategy of plotting the path of every passenger and elevator forward in time before making an allocation lends itself well to a system which has to avoid collisions, and is making decisions about how stopping the car for a new call will impact on other passengers. The TWIN ETD dispatching strategy adds an additional rule set to the basic ETD concept. The rule sets performs two main functions: (i) it holds the back the lower car when the upper car is or will be in the way, and vice versa; (ii) it allows for the lower car to insert calls to move the upper car out of its way, and vice versa. A simplified diagram of the TWIN ETD rule set for the lower car is given in Figure 12.
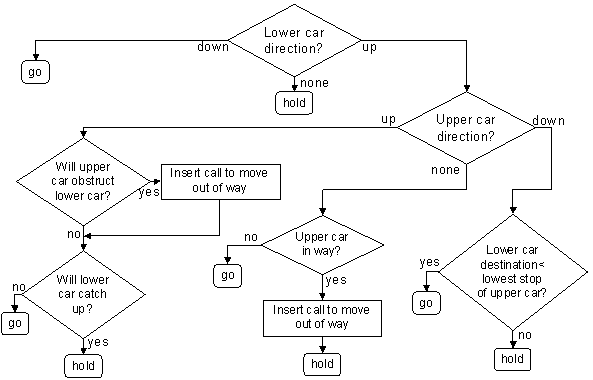
Figure 12 Example rule set for TWIN ETD dispatching
TWIN ETD has been shown to perform well in simulation for all the scenarios proposed to date. This includes: (i) buildings with two entrances where the lower and upper cars are loaded simultaneously; (ii) buildings with single entrances and a virtual landing to “hide” the lower car when the upper car is loading; (iii) zoned solutions where some cars serve different floors; (iv) non-zoned solutions where all cars serve all floors they can physically get to; (v) solutions with lower and upper elevators running at different speeds; (vi) scenarios with TWIN and conventional elevators in the same group.
6. Summary and conclusions
The original ThyssenKrupp ETD concept was presented in a earlier paper, and is now available in a commercial elevator controller. Extensions to the concept allow ETD to take into account the relative importance of waiting and transit times. Additionally, this extension looks at how “painful” each extra second of waiting or transit time is to a passenger. This allows the dispatcher to improve the perceived performance of the system. Other factors can be introduced into the optimization process. It has been shown that energy can be saved purely through dispatching decisions, albeit with a corresponding deterioration in traffic performance.
Vmax is a technology exploiting the fact that most of the time an elevator motor is being under-utilized, as it is not carrying a full load up the building. Traffic performance can be improved by a controlled over-speed of the car.
The ETD concept has also been applied successfully to TWIN, where two cars share a single shaft. Additional rules have been developed to avoid collisions and to coordinate the relative movements of the cars. However, the fundamental ETD concept of modeling the impact of a new call on every other passenger in the system before making an allocation remains the same.
REFERENCES
- Smith R, Peters R ETD Algorithm with Destination Dispatch and Booster Options Elevator Technology 12, Proceedings of ELEVCON 2002 (The International Association of Elevator Engineers) (2002)
- Al-Sharif L, Peters R, Smith R Elevator Energy Simulation Model Elevator Technology 14, Proceedings of ELEVCON 2004 (The International Association of Elevator Engineers) (2004)
- Thumm G A Breakthrough in Lift Handling Capacity Elevator Technology 14, Proceedings of ELEVCON 2004 (The International Association of Elevator Engineers) (2004)
