The Evolution of Lift Traffic Design from Human to Expert System
Gina Barney1 and Richard Peters2
1Gina Barney Associates
2Peters Research Ltd
This paper was presented at The 9th Symposium on Lift & Escalator Technology (CIBSE Lifts Group, The University of Northampton and LEIA) (2018). This web version © Peters Research Ltd 2018.
Keywords: traffic design, expert system, lift, elevator
Abstract. The (human) lift traffic expert solves a number of equations (a mathematical model) to select a suitable lift installation to meet certain design criteria. The expert often then has to adjudicate between several possible designs. This requires a great deal of experience and perspicacity. Many lay people (architects, developers, facility managers, general M&E consultants) and also some lift industry personnel (sales engineers, support staff) desire a simple and quick method of selection.
Over the years there have been many attempts to provide look up tables and charts for a quick selection. This paper describes these historical attempts from the 1960s onwards to the present time. The mathematical models are explained and the design process is described. A demonstration of the design process using a simple spreadsheet presented illustrates the expert decision-making process. The creation of a non-human expert system is discussed in [20].
1. INTRODUCTION
This paper looks at the lift traffic design process applying calculations that a human carries out and whether it can be built into an expert system.
The calculation method uses a mathematical model for uppeak (incoming) traffic and a collective control system to design and evaluate the characteristics of a lift installation. If applied correctly, it determines a lift installation in terms of rated load, rated speed, number of lifts, etc., that generally also meets the requirements of other traffic conditions, such as midday, down peak and interfloor traffic [1]. Furthermore, the calculation method is verifiable, repeatable and reproducible.
The calculation method is based on pure uppeak traffic and uses the classical uppeak analysis equations to determine the two defining design criteria: (1) the lift system handling capacity and (2) the interval. These values can be used to evaluate a lift installation’s ability to meet the Quantity of Service requirement, which is represented by (1) and Quality of Service requirement, which is represented by (2).
In the period from 1965 to 1990 lift traffic designers decided on a value for the required uppeak interval, determined a lift installation that satisfied that value and then calculated the uppeak handling capacity. If the handling capacity was equal or greater than the required value the lift installation was defined.
From ca1990 the requirements were reversed and the lift designer decided on a value for uppeak handing capacity, determined a lift installation that satisfied that value and then calculated the uppeak interval. If the interval was equal or less than the required value the lift installation was defined. This was the first major evolution.
Having carried out a calculation the lift designer might then simulate the chosen lift installation and check parameters such as passenger average waiting times, car loadings, queue lengths, etc.
2. CALCULATION METHOD
The equation that had to be solved to ensure the lift installation could transport the number of passengers arriving in five minutes was and still is:
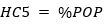
where:
%POP is the passenger demand in persons arriving in five minutes.
HC5 is the lift installation five minute (300 second) uppeak handling capacity in persons per five minutes
The lift traffic designer needs to determine a lift installation that provides a HC5 that is equal or larger than %POP. Thus, to solve Equation (1) a value for HC5 needs to be calculated for the proposed lift installation.
HC5 can be calculated for a single lift from the equation:
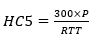
or for a group of L lifts from
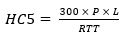
where:
P is the average number of passengers in the car at departure from the main entrance floor.
RTT is the round trip time, in seconds (s), of a single lift during uppeak traffic.
The value of RTT can be calculated from the Equation (4):
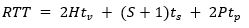
Giving:
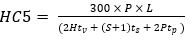
where:
H is the average highest reversal floor
tv is the rated speed of the lift (m/s)
S is the probable number of stops
ts is the time consumed in stopping (s)
P is the average number of passengers in the car
tp is the average passenger transfer time (s)
It will be noticed that the parameter P appears both in the numerator and the denominator of equation (5). This is called a two-point boundary problem. It is solved by the lift designer altering the value of P until Equation (1) is satisfied.
NOTE: The second design requirement (2), the uppeak interval is given by:
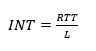
where:
INT is average time, in seconds, between successive car arrivals (or departures) at the main terminal (or other defined) floor
The number of lifts is the prime parameter to meet the second design requirement.
The full elaboration of the mathematics is given in [2]. The following history chronicles a search for a simple process, which hides the mathematics.
3. HISTORY
3.1 1890-1960 Many workers
Lee Gray in his paper [3] presented at the 2017 Lift and Escalator Symposium covered lift traffic analysis up to 1960. It reveals a number of attempts to provide formulae and charts to select a lift installation. These attempts were not taken up by the lift industry and were only known to a very small number of people.
3.2 1967 – Strakosch method
A step change occurred when George Strakosch published Vertical transportation: Elevators and Escalators in 1967 [4]. He provides a manual method to carry out a traffic design, see Table 3. He also utilises a table of probable stops, see Table 1 and a table of lift car occupancy, see Table 2. It is to be noted that all the tabulated numerical values are rounded and he does not statistically evaluate the highest reversal floor and instead uses the top terminal floor as the reversal floor. He was thus unaware of Schroeder’s 1955 work [5]. He does however suggest the design load of a car should be 80% of the Rated Load, see Table 2. In this case, the number of passengers in the car is determined by mass.
Using a spreadsheet, similar figures can be obtained using the data that Strakosch provides, see Appendix 1, column A. The average car occupancy is taken as 80% of the maximum occupancy according to Strakosch Table 4.2 and based on mass.
Strakosch later describes the required handling capacity for a group of lifts (pages 195 et seq) and suitable installations.
In his 1983 book he improves the tables to one place of decimals and argues for more space per person at 0.22 m2 per person. The accepted value today is 0.21 m2 per 75 kg person.
Table 1 Probable Stops (Strakosch Chart 4)
Passengers per trip
| Upper Floors Served |
18 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| 8 | 9 | 10 | 11 | 12 | 13 | 13 | ||
| 16 | 8 | 9 | 10 | 10 | 11 | 12 | 12 | |
| 14 | 7 | 8 | 9 | 9 | 10 | 11 | 11 | |
| 12 | 7 | 8 | 9 | 9 | 10 | 10 | 10 | |
| 10 | 6 | 7 | 8 | 8 | 9 | 9 | 9 | |
| 8 | 6 | 6 | 7 | 7 | 8 | 8 | 8 | |
| 6 | 5 | 5 | 6 | 6 | 6 | 6 | 6 |
Table 2 Lift Car Occupancy (Strakosch Table 4.2 -abstract)
| Capacity (pounds) | 80% Load (people) |
| 2000 | 10 |
| 2500 | 12 |
| 3000 | 16 |
| 3500 | 19 |
| 4000 | 22 |
Table 3 Example of Strakosch calculation procedure
Taken from pages 68-70 of Vertical transportation: Elevators and Escalators, 1967
|
Incoming Traffic Calculations Suppose we want to know how many persons a 3,500 lb elevator at 500 fpm with 3 ft, 6 in center opening doors, in an 11 storey building with 12-ft floor heights, can serve during a 5-min incoming traffic peak period. 1. Table 4.2, page 65, shows that the capacity of a 8500-lb elevator is 19 people. 2. The chart of probable stops, page 64, shows that 19 passengers will make approximately 9 stops on the 10 upper floors in this building. Time to load 19 passengers (Table 4.2): 16.0 sec Time to close 3 ft 6 in. center-opening doors and to start car (Table 4.8): 3.3 sec Time to open the doors when the car returns to the lobby Table 4.4): 0.6 sec Time to start the car and to stop the car when it returns to the lobby: 3.6 sec 3. The total time spent near the lobby: 23.8 sec Time to open the doors at an upper floor stop: 0.6 sec Time to transfer passengers at each upper floor stop: (Table 4.5): 1.8 sec Time to close door at each stop: 3.3 sec Time to start and stop at each stop: 3.6 sec Total time spent at stopping and leaving each upper floor stop: 9.3 sec 4. Nine probable upper floor stops x 9.3 sec per stop equals total stopping time: 83.7 sec 5. Time to run back to first floor from top floor stop and to run from stop to stop exclusive of time required to get up to speed and to stop: 6. Total of all time factors equals round-trip time: 136.0 sec 7. Allowance for inefficiencies 5 percent of items 3 and 4: 5.4 sec Total round-trip time: 141.4 sec Or approximately: 141 sec 8. Elevator 5-min capacity: In other words the single elevator in our example can serve 19 passengers in 141 sec or a total of 40 passengers in 5 min. |
| Item 7, a 5 per cent factor for inefficiency, is added to compensate for the rounding off of probable stops, door time, transfer time, and starting and stopping time and to simplify calculations. It could also be called a confidence factor representing the difference between our assumptions and possible actual conditions. |
3.3 1972 – British Standard Code of Practice CP407
In 1972, the British Standard Code of Practice CP407, Electric, hydraulic and hand powered lifts was published. It contained selection tables, probably calculated by Frank Williams [6] using the Strakosch method and provided values of interval and handling capacity. Example 1 from CP 407 is shown in Table 4.
Table 4 Example from CP 407: 1972
|
Example 1. It is required to design a lift installation in an office building located in the suburbs of a provincial town. It has 8 floors above ground each with 3.3 m pitch (floor-to-floor distance) and 925 m2 in net rentable area. The building will be let to a number of tenants whose starting and leaving times are unlikely to coincide. The population above the ground is given as 740. In the event of the population not being given it should be estimated on the basis of, say, 10 m2 per person. Estimated population above ground 925× 8/10 = 740 persons Since the flow rate is not given it should be assumed as 12%. Required handling capacity per 5 minutes to satisfy 12% flow rate: 740 × 12/100 = 89 persons per 5 minutes The travel of the lift is floors above ground x floor pitch: 8 x 3.3 = 26.4 m From Table 1 [not reproduced in this paper] the car speed required for 26.4 m travel for lifts in offices is 1.5 m/s. Table 2 [reproduced in this paper as Table 5] performance data covers this example of a lift service to ground and 8 floors above, i.e. 9 floors. |
CP 407, Example 1 uses a 12% uppeak arrival rate, which is the currently accepted value. Once the desired handling capacity has been calculated then the CP 407 Table 2 (see Table 5) is used, starting with the number of floors (N+1) to select the number of cars to meet a desired interval.
Example 1 is for a 9 storey building with a required handling capacity of 89 persons/ five minutes. A further table in CP 407 (not shown, Table 1 in that document) suggests three, 16 person lifts giving an interval of 39 seconds.
Many of the design parameters are not provided in CP 407. If following Strakosch then the average occupancy is 80% of the maximum based on mass. Using a spreadsheet a close correspondence for HC5 can be obtained see Appendix A, column B1. The actual %POP delivered is 12.6% and at that demand the interval is 41.1 seconds. If a match is made to 12% then the interval falls to 39.8 seconds, Appendix A, column B2.
Table 5 Passenger Lifts – Performance Data (CP 407: 1972 Table 2)
(Number of floors served: 6, 7, 8, 9). Based on 3.3 m floor-to-floor heights and lifts serving all floors. Standard cars and entrances as shown in BS 2655, Part3
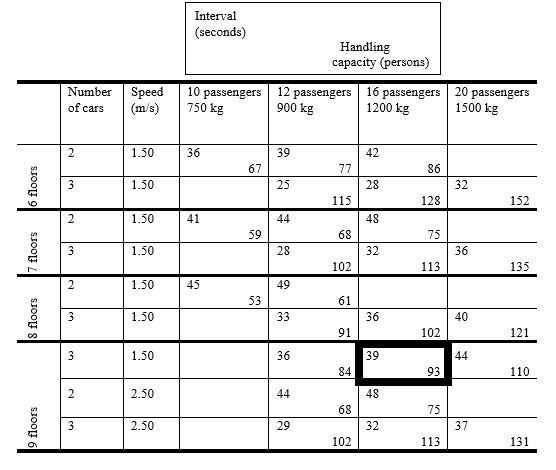
Note: The car sizes are integer values of passengers (persons) and load in kg, as persons times 75 kg precisely.
3.4 1975 – Barney and Dos Santos
In 1975 Barney and Dos Santos [7] developed and published the Round Trip Time (RTT) formula, which followed Strakosch’s work, but including principles from the prior works reported by Gray as:
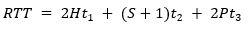
This was the first formulised mathematical model.
This model continues to be widely used today, in a slightly different presentation, by most expert traffic designers, see Equation (4).
3.5 1984 – BS ISO 4190-6
In 1984 ISO published BS ISO 4190-6 “Lifts and service lifts (USA: elevators and dumbwaiters). Passenger lifts to be installed in residential buildings. Planning and selection”. This standard contained selection charts, see Figure 1.
Note the standard only deals with residential buildings and for a passenger demand of 7.5% (%POP). All the user needed to know was the number of floors above the main floor, the population above the main floor and a desired interval. Three values of interval, 60, 80 and 100 seconds (Programme 60, Programme 80, Programme 100).
For example consider a 12 floor building with a population of 425 persons and a desired interval of 100 seconds. Using the chart then the lift installation could be either , or .
Configuration 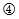
Configuration 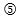
Configuration 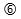
This is where the human designer has to use their expertise in order to choose between the three possibilities.
These graphs are very broad-brush. For example, consider the Programme 80 without parking level. Take a building with 10 floors and a population of 400 persons. The suggested lift installation is 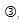
There are no details of the mathematics, but the procedures probably follow Strakosch. A peculiarity of the standard is the unequal rated load combinations. These graphs were often used by lift industry sales people.
An important point is the ISO 4190-6 standard states clearly in its Table 2 that the average car occupancy is to be 80% of the maximum based on rated load (mass).
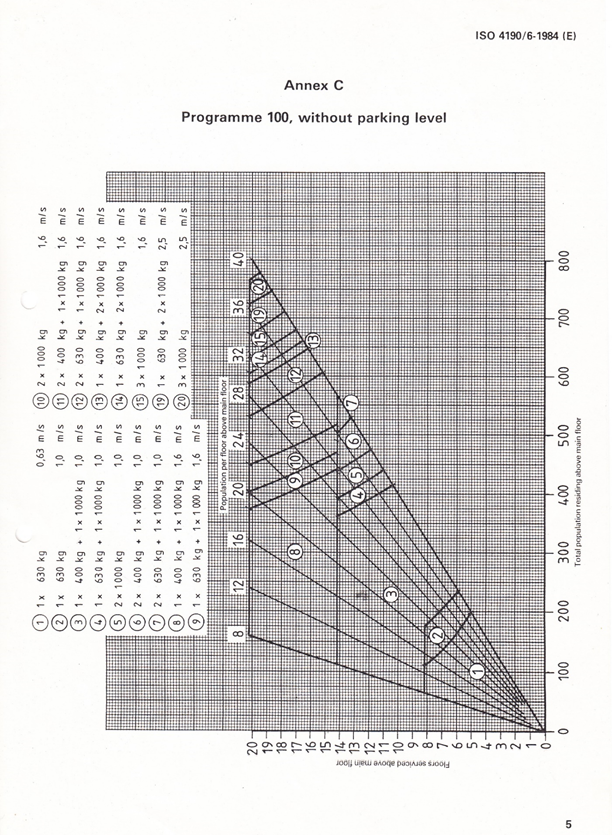
Figure 1 Selection graph from ISO 4190-6: 1984
3.6 1988 – Elevator Micropedia
In 1988 the first edition of the Elevator Micropedia [8] was published. This included a “Ready Reckoner”, see Table 6. The lift industry has been and still is a very pragmatic industry and mathematics is an art few are comfortable with. Hence the inclusion of a ready reckoner.
The ready reckoner was developed for the performance of one lift and automates the calculation of the round trip time. All the necessary input data is specified.
Table 6 Sample page from Elevator Micropedia 1988
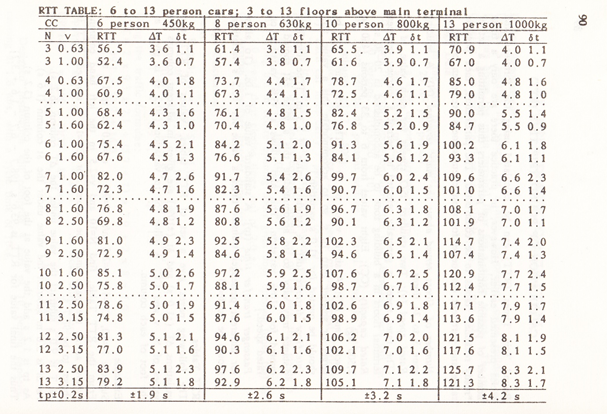
The ready reckoner offers the user the opportunity to vary the “cycle time” (today called “performance time”) by ±1.0 s, the interfloor distance by ±10% and the passenger transfer times by ±0.2 s.
Example
Find the handling capacity of a lift system serving a ten floor building with a 10 person car (contract capacity 800 kg), a contract speed of 2.5 m/s, a performance time (T) of 9.0 s, an interfloor distance of 3.0 m and an assumed passenger transfer time of 1.2 s.
Using the Table find N =10 and v = 2.5 in the left hand column.
Follow across the page until the column for CC = 10 is reached. The RTT is shown as 98.7 s.
As T is 9.0 s subtract the value under ΔT column (6.7 s).
As df is 3.0 m subtract the value under the δt column (1.6 s).
As tp is 1.2 s add the value at the foot of the column (3.2 s).
Thus the final value for RTT is 93.6 s (98.7 – 6.7 – 1.6 +3.2).
Using equation (3)
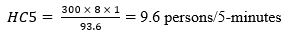
Note the number of passengers in the car are by mass, not area.
The ready reckoner tables were included in CIBSE Guide D: 1993[9]. They did not appear in CIBSE Guide D: 2000 as by then calculations were being carried out where the average number of passengers in a lift car was determined by area not mass.
4 PASSENGER CAPACITY BY MASS OR AREA?
Passengers will not usually board a crowded car, especially if the other passengers are strangers. Strakosch in his 1967 book observed the loading of lift cars did not meet the assumed loading based on weight. Fruin [10] (1971) drew a person template with a body ellipse of 600 mm by 450 mm, which is 0.21 m2. Thus an anomaly between the stated passenger capacity (in persons), displayed on the in-car rating plate and the actual number of passengers observed in a car developed. In 1993 edition of CIBSE Guide D[9], an actual value for passenger capacity was shown in Table 3.4 based on a body ellipse of 0.2 m2 and a 5% reduction for handrails, etc., ie: 0.21 m2.
Perceptively the ISO Technical Report ISO/TR 11071-2, 1996 [11] [repeated in 2006] said:
“While the entire subject of capacity and loading has historically been treated in safety codes as one and the same, it might be more meaningful in the future writing of safety codes to cover loading as a separate issue from capacity. One refers more appropriately to the traffic handling capacity, whereas the other refers to the maximum carrying capacity which has a direct bearing on safety.”
The scepticism of this change from mass to area in calculating car occupancy gradually disappeared as various designers [12][13] confirmed it. The latest editions of the British Council of Offices guidelines [14] recommend area based car selection.
Calculation of the number of passengers by area rather than by mass is now accepted best practice, used in the industry de facto standard simulation software [15] and readily available spreadsheets [16]. All competent traffic designers now use area.
In conclusion it is important to size lifts to fit people, not to weigh them. That is, a method based on providing the personal space, which is comfortable for a person to occupy. This method has replaced the previous method using weight (mass) over a period of evolution commencing in the 1990s until the present time. This was the second major evolution.
5 2014 – REVISION OF ISO 4190-6: 1984 {ISO 8100-32}
In 2014 the International Standards Organisation, Technical Committee 178, formed Sub Group 5 in its Working Group 6, to revise BS ISO 4190-6: 1984. WG6 takes the view that equations and the design process is too difficult for a lay person to apply. SG5 has published revised versions of the charts of 1984 for public comment and extended them to include offices and hotels. Consider Figure C.1 (shown as Figure 2) in the draft sent out for comment in 2018.
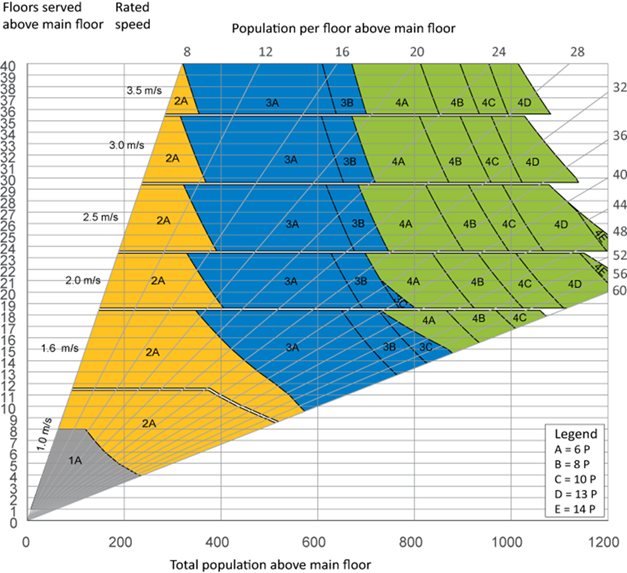
Figure 2 Figure C.1 from draft ISO 8100-32
The charts are created following the methodology presented by Ruokokoski and Siikonen [17].
Note: the calculation used for these charts is based on formulae in the draft ISO 8100-32 rather than those given in this paper.
The charts are complex to draw, which is reflected in the simplification of the inputs selected. For example, a 2.0 m/s lift is only considered for buildings with 19 to 23 floors; it would not be unreasonable to consider a 2.0 m/s lift for an 18-floor building. This could mean the designer selects a four-lift solution when a three-lift solution would be adequate.
Regions overlap, so choosing which region is displayed is a matter of judgement. For example, the 1A region is cut off at 8 floors. In fact, it continues, up to 10 floors, hidden by the 2A region. So, for a building with 10 floors served above the main terminal and a total population of 100, one 6-person lift meets the criteria, but the graph is suggesting two 6-person lifts.
Another challenge when creating these graphs is that some regions are too small to be labelled.
An approach which plotted the boundary lines rather than regions would have the advantage of not hiding prospective solutions from the user [20].
6 2017 – PROPOSAL – GRAPHS BASED ON P THE AVERAGE CAR LOADING
Much of this discussion has been dominated by the number of persons that need to be accommodated (by area) in the lift car. Once the number of passengers to be accommodated is known then a suitable sized lift car can be selected from Table 7.
Table 7 Rated load, maximum available car (platform) area, maximum passenger capacity (Pmax) and average passenger capacity (P)*
|
Rated load |
Maximum available car area (m2) |
Passenger capacity Pmax and P by area @ 0.21 m2 per person |
|
| Pmax | P | ||
| 450 | 1.30 | 6.2 | 5.0 |
| 630 | 1.66 | 7.9 | 6.3 |
| 800 | 2.00 | 9.5 | 7.6 |
| 1000 | 2.40 | 11.4 | 9.1 |
| 1275 | 2.95 | 14.0 | 11.2 |
| 1350 | 3.10 | 14.8 | 11.8 |
| 1600 | 3.56 | 17.0 | 13.6 |
| 1800 | 3.88 | 18.5 | 14.8 |
| 2000 | 4.20 | 20.0 | 16.0 |
| 2500 | 5.00 | 23.8 | 19.0 |
* P = 80% of Pmax. Assumes a capacity factor of 80%.
However, most designs start with the number of floors in a building and the population. This has led to the development of the chart shown in Figure 3. This chart has been produced manually.
For example, suppose a lift installation is to be selected for an office building with eight floors above the entrance floor and a population of 2000 persons. The circled result shows that there is a choice of either 8 x 1800 kg (which is about right) or 8 x 2000 kg (which provides extra capacity) or 7x 2500 kg (which requires less lifts).
7 2017 – A BASIC EXPERT SYSTEM
Barney, Peters and Dean [18] produced a set of tables using an expert engine with a range of parameters to include in an alternative draft for ISO 8100-32 [19]. The expert system mimics a design methodology specified by Barney, incorporating design choices made where guides and standards require the reader to interpret a requirement or make a choice. The process of developing the expert engine itself took several iterations as additional rules were added to account for judgements the designer is called to make in the design process. The creation of this expert system is discussed in the paper Expert Systems for Lift Traffic Design [20].
8 CONCLUSIONS
The selection of a lift installation requires mathematical modelling, experience and judgement. Reducing the whole selection process to a graph, table or software requires choices and assumptions to be made by the person creating the tool. These assumptions may be incorrect even for the most sophisticated expert system unless the expert has ensured the software is asking all the right questions, and all assumptions made are fully understood by the person using the tool.
De-skilling engineers by providing graphs, tables and expert systems has risks. Yet hiding the mathematics and encapsulating experience and judgement in a design tool is repeatedly called for, and the development of increasingly sophisticated expert systems is inevitable. In an industry where “experts” often do not agree, expert systems will also not agree.
REFERENCES
- Barney, Gina, 2003, “Elevator Traffic Handbook”, Taylor & Francis, §15.3
- CIBSE Guide D: 2015, “Transportation systems in buildings“, CIBSE
- Gray, L.E., “Lift traffic analysis 1880 – 1960“, Lift and Escalator Symposium, 2017
- Strakosch, G.R., 1967, “Elevators and escalators“, 1/ed, Wiley
- Schroeder, J., 1955, “Personenaufzuege (passenger lifts)“, Foerden und Heben, 1 (in German)
- Williams, F.H., 1972, “Selection of passenger lifts for office buildings“, Architects Information Library, August 1972, pp 331 – 332
- Barney, G.C. and Dos Santos, S.M., 1975, “Improved traffic design methods for lift systems“, Bldg. Sci.
- Barney G, 1988, “Elevator Micropedia“, International Association of Elevator Engineers, 1988, ISBN 0951349813, 9780951349816
- CIBSE Guide D: 1993, “Transportation systems in buildings“, CIBSE
- Fruin, J.J. 1971, “Pedestrian planning and design“, Metropolitan Association of Urban Designers and Environmental Planners
- ISO/TR 11071-2:1996, “Comparison of worldwide lift safety standards – Part 2: Hydraulic lifts“
- Day, P. 2001a, “Passenger comfort – Are you travelling comfortably?“, Elevator World, April. 2001
- Day, P. 2001b, “Lift passenger comfort have we got it right?“, Elevatori, September 2001
- British Council for Offices, 2014, “Guide for Specification“, BCO
- Elevate traffic analysis and simulation software, www.peters-research.com, accessed 20 July 2018
- Lift Traffic Design Spreadsheet, www.bit.ly/lifttrafficspreadsheet, accessed 20 July 2018
- Ruokokoski M, Siikonen, ML, “Lift Planning and Selection Graphs” Proceedings of the 7th Symposium on Lift & Escalator Technology 2017
- Barney, Gina and Peters, Richard, Dean, Sam, Private Communication/software
- Barney, Gina and Peters, Richard, “An alternative draft for ISO 8100-32“, March 2017.
- Peters, Richard and Dean, Sam, “Expert Systems for Lift Traffic Design“, Proceedings of the 9th Symposium on Lift & Escalator Technology 2018
BIOGRAPHICAL DETAILS
Dr Gina Barney Principal of Gina Barney Associates, English Editor of Elevatori, Member of the Chartered Institution of Building Services Engineers (CIBSE) Lifts Group Committee, Member of the British Standards Institution (BSI) Lift Committees, UK expert to two International Standards Organisation groups. Dr Barney is the author of over 100 papers and is the author, co-author or editor of over 20 books. She has the degrees of BSc, MSc and PhD and the professional qualifications of CEng, FIEE, HonFCIBSE and Eur.Ing.
Richard Peters has a degree in Electrical Engineering and a Doctorate for research in Vertical Transportation. He is a director of Peters Research Ltd and a Visiting Professor at the University of Northampton. He has been awarded Fellowship of the Institution of Engineering and Technology, and of the Chartered Institution of Building Services Engineers. Dr Peters is the author of Elevate, elevator traffic analysis and simulation software.
Appendix A – Spreadsheet Examples
| A | B1 | B2 | |
| INPUT DATA | Value | Value | Value |
| Number of floors | 10 | 8 | 8 |
| Rated load | 1590 | 1600 | 1600 |
| Actual car capacity | 21 | 16 | 16 |
| Number of passengers | 19 | 12.8 | 11.8 |
| Number of lifts | 1 | 3 | 3 |
| Rated speed | 2.5 | 1.5 | 1.5 |
| Building population | 180 | 740 | 740 |
| Interfloor distance | 3.6 | 3.3 | 3.3 |
| Express jump | 0 | 0 | 0 |
| Express additional time | 0 | 0 | 0 |
| Single floor flight time | 5.1 | 4.9 | 4.9 |
| Door close time | 3.3 | 3.2 | 3.2 |
| Door open time | 0.6 | 2.5 | 2.5 |
| Advance door opening | 0 | 0 | 0 |
| Start delay | 0.85 | 0 | 0 |
| Passenger transfer time | 0.84 | 1 | 1 |
| RESULTS | Value | Value | Value |
| Number of passengers | 19.0 | 12.8 | 11.8 |
| Highest reversal floor | 9.85 | 7.79 | 7.76 |
| Number of stops | 8.65 | 6.55 | 6.35 |
| Performance time | 9.9 | 10.6 | 10.6 |
| Round trip time | 141.4 | 123.3 | 119.4 |
| Interval | 141.4 | 41.1 | 39.8 |
| Handling capacity | 40 | 93 | 89 |
| Percentage population | 22.4 | 12.6 | 12.0 |
| Capacity factor (%) | 90 | 80 | 74 |
| Uppeak average waiting time | 161 | 35 | 28 |
| Down peak handling capacity | 63 | 146 | 139 |
| Midday peak handling capacity | 48 | 118 | 113 |
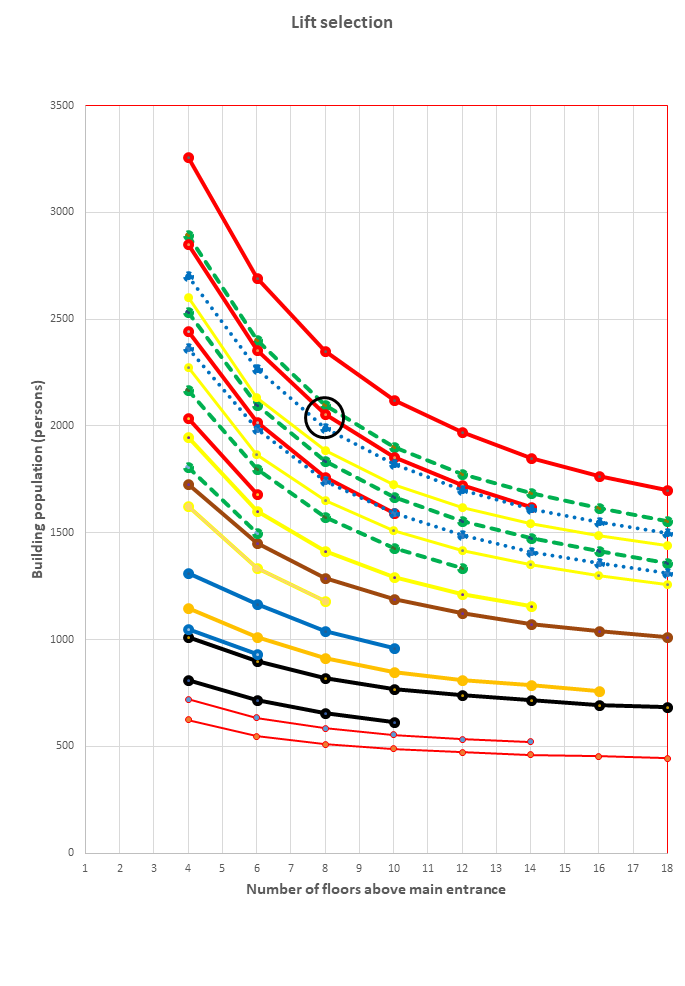
Figure 3 Example graphical presentation of expert system results

