The Theory and Practice of General Analysis Lift Calculations
R D Peters BSc
Ove Arup & Partners
This paper was presented at ELEVCON Amsterdam 1992, The International Congress on Vertical Transportation Technologies and first published in the IAEE book “Elevator Technology 4”, edited by G.C. Barney. It is reproduced with permission from The International Assocication of Elevator Engineers. This web version © Peters Research Ltd 2010.
Abstract
The formulae presented in this paper allows analysis of any peak passenger traffic flow for any practical configuration of lifts. This means that we can consider not only a typical office morning up peak, but also shopping centres, office blocks with underground car parks and roof top restaurants, etc – scenarios not dealt with by traditional lift traffic analysis methods. Derivation of the formulae and their implementation on a personal computer are discussed. Practical applications are demonstrated using the Oasys LIFT program which utilises the General Analysis formulae. Examples are taken from projects on which the author has advised.
1. Introduction
Many engineers designing with the help of computers have a healthy scepticism of complex computer models which sometimes give unrealistically precise predictions of our imprecise world.
But it is possible and worthwhile to learn about the effects on lift service of any passenger lift traffic flows where they can be predicted for a new building or measured in an existing building.
Analytical lift calculation procedures generally address specific passenger traffic flows. An up peak analysis describes the morning incoming peak in an office building, a down peak the reverse. A two way peak describes a combination of up and down peak traffic (e.g. the traffic flow in a multistorey car park). The interfloor analysis allows passengers to arrive at any level, but assumes their destinations are always in proportion to the individual floor populations. Each of these traffic flows are solely special cases for the General Analysis procedure described in this paper which, when implemented on a computer, allows analysis of any peak passenger flow for any practical configuration of lifts.
Before considering the General Analysis formulae we must first define our measure of passenger traffic. The term commonly applied in an up peak analysis, the Five Minute Ratio, cannot describe fully the traffic we wish to define.
2. Defining lift passenger traffic
The author’s introduction to lift traffic analysis was through writing a lift simulation program, as noted in the biography of this paper. Any analytical analysis for the general case must define lift passenger traffic in a similar way to simulation models, identifying the rate of passenger arrivals at each lift landing station and the passengers’ probable destinations. To define the passenger flow completely we need two terms:
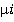 the passenger arrival rate at floor i (defined for each floor at which passenger may arrive)
the passenger arrival rate at floor i (defined for each floor at which passenger may arrive)
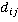 the probability of destination floor of passenger from floor i being the jth floor (defined for all possible i and j)
the probability of destination floor of passenger from floor i being the jth floor (defined for all possible i and j)
It is easier to show these terms diagrammatically. For example the simple case of an up peak traffic flow in an office block could be as shown in figure 1.
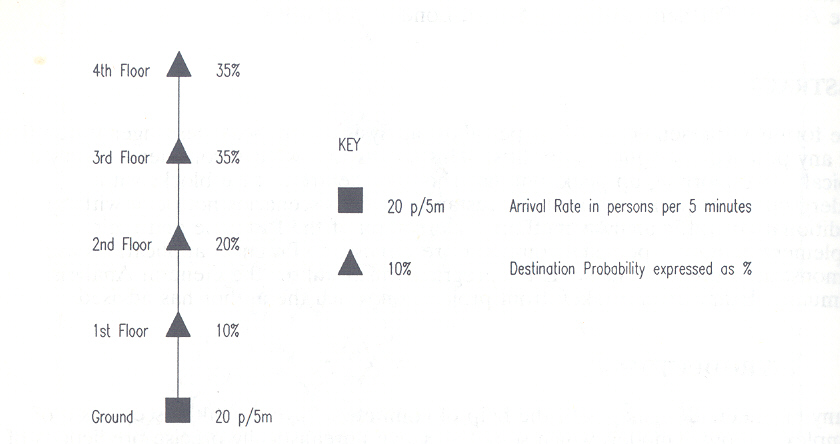
Figure 1 Example passenger traffic flow for a typical office up peak
A more complex traffic flow such as may be found in a shopping centre with car park above could be as shown in figure 2
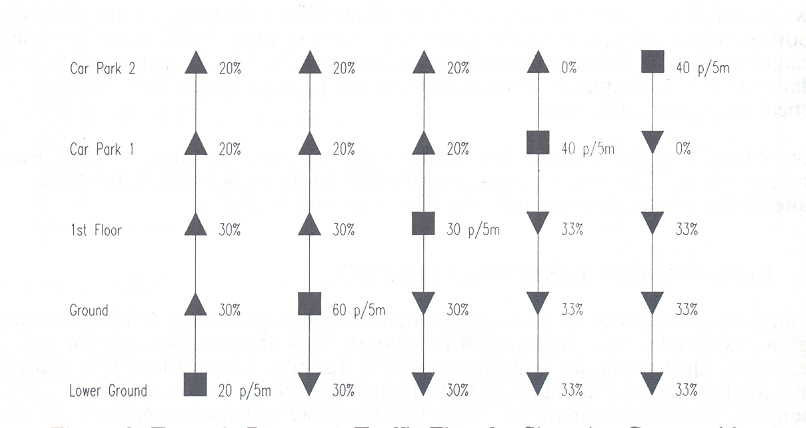
Figure 2 Example Passenger Traffic Flow for Shopping Centre with Car Park above
3. Principles of derivation
Having defined passenger traffic we can apply our mathematical model. It is not the intention of this paper to give a line by line derivation of the formulae, but to establish the basic principles and assumptions. The complete set of formulae and definitions are given in the appendix of this paper. The formulae were first published by the CIBSE Building Services Engineering Research and Technology Journal in 19901.
Before we write down the formulae we must define one more term:
Pij(n) Probablility of n passengers travelling from the i th to the j th floor in the time interval T
It is generally accepted that the arrival of passengers at a lift landing station is reasonably approximated by a Poisson process2. This gives us the result:
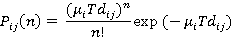
When dealing with probabilities it is generally easier to calculate the probability of an event not happening, and subtract that result from 1 to find the probabiity of the event. So, if we let
Pij = Pij(0)
we get:
Pij= exp(-µi Tdij)
The probability of the lift stopping at the jth floor on its journey up is:
1 – (probability of no calls from lower floors to the jth floor) * (probability of no calls from the jth floor to higher floors)
Mathematically, we can express this:

Applying this and similar principles we can derive
S the probable number of stops in a round trip
L the probable lowest reversal floor
H the probable highest reversal floor
For more complex problems where lifts do not serve all the same floors, or are of different speeds, capacities, etc we must define “overlapping zones” where passengers are likely to take the first lift that arrives and serves their destination floor. The formulae allow us to calculate the split of traffic between overlapping zones for each possible journey from the ith to the jth floor.
4. Computer implementation
A standard IBM PC or compatible has sufficient computing power to calculate a solution for a typical lift configurtion within seconds.
Implementation of the method is relatively straightforward for someone with experience of lift traffic analysis and computer programming. As is the case for many analytical programs, writing the user input/output routines can be the most difficult and time consuming task.
The calculation is iterative as the equations for probable number of stops and reversal floors are dependant on the Waiting Interval and vice-versa. the procedure here is to “guess” the Waiting Interval, revising the guess for each iteration until the guess equals the result.
The flow chart in figure 3 defines the main program structure and subroutines.
A further iteration is required if overlapping zones are defined as the calculation for splitting data between zones is dependant on the Waiting Interval of each zone and vice-versa.
5. The Oasys LIFT program
The Oasys (Ove Arup Computing Systems) LIFT program has been used on a wide range of projects throughout the international Ove Arup Partnership since its first issue in 1989.
The program is written in Fortran 77 with the help of Oasys standard input/output routines and run on PC’s.
In addition to basic implementation of the General Analysis method, the program offers the user additional features:
- the computer automatically calculates destination probabilities for specific passenger traffic flows such as up peak, down peak, two way and interfloor when selected by the user
- for the defined passenger traffic, the program will allow analysis over a range of possible solutions in a single analysis run (e.g. 3 to 4 lifts, 1.6 to 2.5m/s, etc)
- a traditional up peak analysis calculation procedure is included and allows users to compare results and confirm consistence before considering more complex traffic flows with the General Analysis method
From the users viewpoint there is one main difference between using the traditional (OLD) and General (NEW) calculation procedure for an up peak analysis: in a traditional analysis you would normally assume that the lift was 80% full and calculate the resultant Five Minute Ratio. Using the General Analysis method the Five Minute Ratio is defined and the program determines how full the lift is as a result of this passenger traffic.
Figure 3 Program Flow Chart
The second approach is more helpful as specifiers often choose larger lifts than required for reasons of prestige, etc which if assumed 80% full give unrealistically high Five Minute Ratios and Waiting Intervals. The General Analysis just notes how full the lift is for the given Five Minute Ratio.
One occasional user problem is that zero Waiting Interval and Capacity Factor results are given when the program is asked to analyse an over-lifted solution. If there is insufficient traffic to keep the lifts busy, in effect there will normally be a lift left waiting at the main terminal floor unused – the iterative value of Waiting Interval tends to zero, as would be the case in real life.
6. Examples
6.1 A typical office up peak analysis
A prestigious office block in London with ground floor and eight upper stories. Floor populations range between 50 and 100 persons per floor. A stair factor of 50% (50% walk one floor, 25% two, 13% three, etc) has been assumed.
The morning up peak is likely to be the busiest time for the lifts. A five Minute Ratio of 17% is assumed based on the possiblity of an unified tenancy with the majority of employees starting work in the morning at approximately the same time.
The user enters the data, selecting the up peak analysis (so not needing to define destination probabilities which are in proportion to the population of each office floor). The lift analysis selection criteria is set over a range of numbers of lifts, capacities, speeds, etc with limits defined for the maximum Waiting Interval and Capacity Factor acceptable.
Each configuration is analysied, rejected or displayed dependant on whether or not the selection criteria are met. The user selects his preferred solution from the output, in this case:
No of lifts 3
Contract Speed 2.0m/s
Lift Capacity 1000kg
Probable No of Stops 6.4
Probable Highest Reversal floor 7
Waiting Interval 30s
Capacity Factor 70%
For this “simple” case the user could compare results with the alternative, traditional up peak analysis. Here the default Capacity Factor is 80% and the Five Minute Ratio is calculated as opposed to input. The results are as follows:
No of lifts 3
Contract Speed 2.0m/s
Lift Capacity 1000kg
Waiting Interval 33s
Five Minute Ratio 18%
The results are very similar for both analysis methods. The second set of results have marginally higher Waiting Interval and Five Minute Ratio, but this corresponds with the lift being 80% as opposed to 70% full for the round trip.
Having demonstrated consistence for an up peak analysis between the General Analysis and a traditional calculation methods, we will now consider a more complex traffic flow.
6.2 Lunchtime peak at office block with roof top restaurant
Again a prestigious office block (with lower ground, ground and 6 upper floors), but this time the architect has suggested locating the office restaurant/cafeteria on the top floor. The lifts are satisfactory to cope with the morning up peak, but will they cope with the lunchtime peak?
In this case the lunchtime peak is likely to be made up of a combination of:
- passengers travelling from their offices to the roof top restaurant for lunch
- passengers travelling back to their offices after lunch at the restaurant
- passengers travelling to the ground floor to leave the building to buy sandwiches or eat out
- passengers returning from buying/eating out
The estimate of the combined traffic flows early during the lunch hour was as shown in figure 4 (less people are expected to travel within a five minute period than during the morning up peak).
Figure 4 Summation of lunchtime peak passenger flows for office block with restaurant on top floor
The analysis gives the following results:
No of lifts 3
Contract Speed 2m/s
Waiting Interval 34s
Capacity Factor (1250kg) 23%
Probable No of stops 8.6
Probable Lowest Reversal floor G
Probable Highest Reversal floor Restaurant
The lifts always reach the top floor during their round trip, unlike during the up peak. Lifts are also stopping regularly during their journey down rather than expressing to the ground floor, another delay.
In this case the lifts can cope with the specified traffic flow, but the service is poorer than during the morning up peak.
7. Current developments
The theory has been extended to incorporate double decker lifts and is currently being implemented within the Oasys LIFT program. The formulae will be published in due course.
8. Conclusions
The General Analysis gives us a tool to analyse any peak passenger traffic flow quickly and effectively. Analytical as opposed to the more comlex and computer power-hungry simulation models are likely to be our basic lift traffic analysis tools for the foreseeable future. The writer proposes this General Analysis method for implementation as a total solution for analysis of all peak passenger traffic flows.
We need to define clearly expected passenger traffic before embarking on a detailed analysis, and interpret results remembering the limited accuracy of our input data. There appears to be little published data detailing surveys of lift passenger traffic flows – this needs to be addressed if we are to make full use of our new passenger traffic analysis tools.
REFERENCES
- Peters R D CIBSE Building Srevices Engineerin gResearch and Technology Volume 11 Number 2 (1990)
- Barney G C and dos Santos S M Elevator Traffic Analysis Design and Control 2nd edn (London: Peter Peregrinus)(1985)
APPENDIX – General Analysis formulae
A List of symbols
| µi | Passenger arrival rate at floor i (persons s-1) |
| dij | Probability of the destination floor of a call from i being the jth floor |
| T | Waiting interval (s) |
| N | Number of floors |
| Pij(n) | Probability of n passengers travelling from the ith to the jth floor in the time interval T |
| Pij | Probability of no calls from the ith to the jth floors in the time interval T |
| pS1 | Probability that a lift will stop at lowest floor |
| pUS2, pUS3,….pUSN-1 | Probability that the lift will stop at each of the intermediate floors on its journey up |
| pSN | Probability that the lift will stop at the hightest floor, N |
| pDSN-1,…PDS2 | Probability that the lift will stop at each of the intermediate floors on its’ journey down |
| S | Probable number of stops |
| pHn | Probability of nth floor being the highest reversal floor |
| pLn | Probability of nth floor being the lowest reversal floor |
| H | Highest reversal floor |
| L | Lowest reversal floor |
| JWI(i,j) | Journey waiting interval for passengers travelling from the ith to the jth floor(s) |
| T(n) | Waiting interval, zone n |
| SPLIT (Q,i,j) | Proportion of passengers travelling from the ith to the jth floor who are using lifts in zone Q |
B Call Probabilities
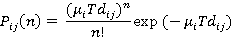 (1)
(1)
Pij = exp(-µi Tdij) (2)
C Probable number of stops
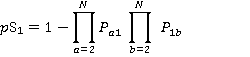 (3)
(3)
 (4)
(4)
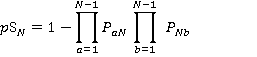 (5)
(5)
 (6)
(6)
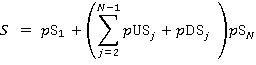 (7)
(7)
D Highest Reversal Floor
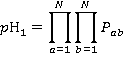 (8)
(8)
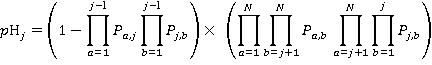
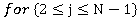 (9)
(9)
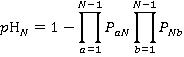 (10)
(10)
A good check for this is: 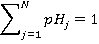
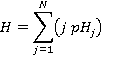 (11)
(11)
E Lowest reversal floor
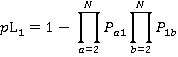 (12)
(12)
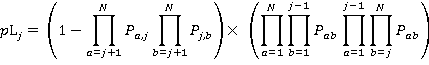
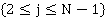 (13)
(13)
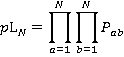 (14)
(14)
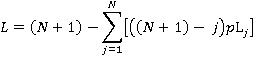 (15)
(15)
F Passengers in car calculation – eg ith floor journey up
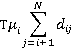 passengers enter the car
passengers enter the car
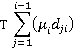 leave the car
leave the car
G Overlapping Zones
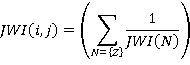 (16)
(16)
{Z} = {all zones serving both the i th and the j th floor}
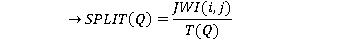 (17)
(17)
